Rational Numbers- Rational numbers are a fundamental concept in mathematics. They are a subset of the real numbers and can be expressed as the quotient or fraction of two integers, where the denominator is not equal to zero. In other words, a rational number can be written as a/b, where “a” and “b” are integers, and “b” is not equal to zero.
Examples of rational numbers include:
- 1/2
- 3/4
- -5/2
- 7/1 (which is just 7)
- 0 (0 can be represented as 0/1)
Rational numbers can be positive or negative and can include both whole numbers and fractions. They can be finite (terminating) or infinite (repeating) decimals. For instance:
- 0.25 (a finite decimal)
- 0.333… (repeating decimal, also represented as 1/3)
- 0.142857142857… (repeating decimal, also represented as 1/7)
The set of rational numbers is denoted by the symbol “Q.” It is an important concept in mathematics and finds applications in various fields, including algebra, geometry, and real analysis. The operations of addition, subtraction, multiplication, and division can be performed with rational numbers, and the result will always be another rational number, except in the case of division by zero, which is undefined.
What is Required Class 8 Mathematics Rational Numbers
In Class 8 Mathematics, the topic of Rational Numbers is an essential part of the curriculum. Students learn about rational numbers in detail, including their properties, operations, and applications. Here are some of the key concepts covered under Rational Numbers in Class 8:
- Introduction to Rational Numbers: Students are introduced to the concept of rational numbers and how they can be represented as fractions a/b, where “a” and “b” are integers and “b” is not equal to zero.
- Properties of Rational Numbers: Various properties of rational numbers are taught, such as closure property under addition, subtraction, multiplication, and division. Students also learn about the commutative and associative properties of addition and multiplication for rational numbers.
- Representation of Rational Numbers on the Number Line: Students learn to represent rational numbers on a number line to understand their order and relative magnitude.
- Operations with Rational Numbers: Addition, subtraction, multiplication, and division of rational numbers are covered in detail. Students practice solving problems involving these operations with both positive and negative rational numbers.
- Simplification of Rational Numbers: Students learn how to simplify or reduce fractions to their lowest terms.
- Mixed Numbers and Improper Fractions: The concept of mixed numbers and improper fractions is introduced, and students learn how to convert between these two representations.
- Comparison of Rational Numbers: Students are taught how to compare rational numbers and order them from least to greatest or greatest to least.
- Word Problems Involving Rational Numbers: Real-life word problems are presented, where students need to apply their understanding of rational numbers to solve them.
The study of rational numbers in Class 8 lays the foundation for more advanced topics in mathematics, particularly in algebra and higher-level arithmetic. Understanding rational numbers is crucial for future concepts like solving equations, inequalities, and working with polynomials. It is essential for students to have a solid grasp of these concepts as they progress in their mathematical journey.
Where is Required Class 8 Mathematics Rational Numbers
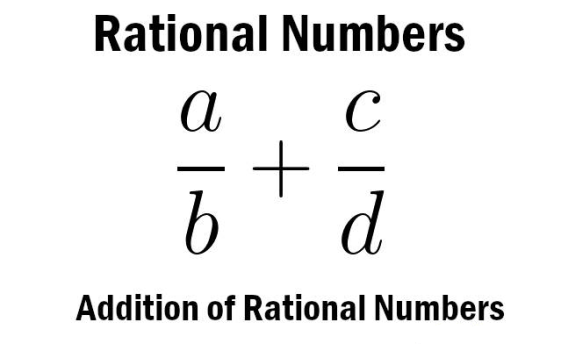
It is a part of the academic syllabus for students around the age of 13-14 years, depending on the educational system and country.
In educational institutions, Class 8 Mathematics is usually taught as a part of middle school or secondary education. The topic of “Rational Numbers” is a specific chapter or unit within the mathematics textbook for Class 8.
The content and structure of the Class 8 Mathematics curriculum, including the topic of Rational Numbers, vary from one educational board or country to another. However, the concepts covered are generally similar, as outlined in the previous response.
If you are a student studying in Class 8 or a parent/guardian seeking resources to help with the topic of Rational Numbers, you can find relevant textbooks, study materials, and online resources from educational bookstores, school libraries, or reputable websites specializing in educational content. Many online educational platforms also offer video tutorials and practice exercises on this subject to enhance students’ understanding.
Application of Class 8 Mathematics Rational Numbers
Rational numbers have numerous practical applications in everyday life and various fields of study. Some of the key applications of Class 8 Mathematics Rational Numbers are as follows:
- Measurements and Scaling: Rational numbers are used to represent measurements in real-life scenarios. For example, when measuring length, weight, volume, or temperature, we often encounter fractional values like 3.5 meters or 2.25 liters.
- Finance and Banking: Rational numbers are essential in financial calculations, such as interest rates, discounts, and percentages. For instance, calculating interest on a loan or the markup on a product involves working with fractions and decimals.
- Cooking and Recipes: In cooking, recipes often require measurements that involve rational numbers, such as 1/2 cup of flour or 3/4 teaspoon of salt.
- Stock Market and Investments: Rational numbers are used to represent stock prices, changes in stock values, and investment returns.
- Maps and Navigation: Maps and navigation systems use rational numbers to represent distances, coordinates, and directions.
- Time and Clocks: Rational numbers are used to represent time, such as 3:30 PM, 4:45 AM, etc.
- Science and Engineering: Rational numbers are used in various scientific and engineering calculations, such as in physics, chemistry, and engineering disciplines.
- Probability and Statistics: Rational numbers are employed in probability and statistics to represent probabilities, fractions, and percentages.
- Geometry and Measurements: Rational numbers are used in geometry to represent measurements, angles, and sides of shapes.
- Scale Drawings: Rational numbers are used to scale down or up objects in scale drawings, such as blueprints and architectural plans.
- Sports and Games: Rational numbers are used in sports statistics, such as batting averages, winning percentages, etc.
- Medicine and Health: Rational numbers are used in medical dosage calculations, blood pressure readings, and other health-related measurements.
These are just a few examples of how rational numbers are applied in real-life situations and different academic disciplines. Understanding and working with rational numbers are essential skills that enable individuals to solve various problems and make informed decisions in their daily lives and professional careers.
Case Study on Class 8 Mathematics Rational Numbers
Rational Numbers in Everyday Life
Name: Sarah Age: 13 Grade: Class 8
Background: Sarah is a 13-year-old student studying in Class 8 at a middle school. She has always been interested in mathematics and finds it fascinating to see how mathematical concepts apply to real-life situations. Recently, her mathematics class started the topic of Rational Numbers, and she was excited to learn more about it.
Challenge: As Sarah progressed through the Rational Numbers chapter, she faced some challenges in understanding certain concepts. Specifically, she found it difficult to grasp the concept of converting between mixed numbers and improper fractions. Additionally, she struggled to visualize how rational numbers can be represented on a number line and ordered from least to greatest.
Approach: Sarah’s mathematics teacher recognized her enthusiasm for the subject and decided to take a hands-on approach to help her overcome the challenges. The teacher designed a case study to demonstrate the practical applications of rational numbers in Sarah’s everyday life.
- Cooking and Baking: The teacher brought in various ingredients and recipes, including flour, sugar, butter, and recipes for cookies and cakes. She asked Sarah to measure and mix the ingredients according to the given fractions in the recipe. This exercise helped Sarah understand how rational numbers are used in cooking and baking.
- Shopping Discounts: The teacher gave Sarah a list of items with their original prices and the discounts offered on each item. She asked Sarah to calculate the discounted price of each item using rational numbers, fractions, and percentages. This activity illustrated the use of rational numbers in real-life shopping scenarios.
- Map Scale and Distance: The teacher provided a map of Sarah’s neighborhood and asked her to measure the distances between various locations using the given scale. Sarah learned how rational numbers and scale are used in map representations.
- Time and Scheduling: The teacher presented Sarah with a schedule of daily activities and asked her to convert the given time from 12-hour format to 24-hour format. This exercise helped Sarah comprehend the practical applications of rational numbers in time representation.
Outcome: Through the case study and hands-on activities, Sarah’s understanding of rational numbers improved significantly. She became more confident in converting between mixed numbers and improper fractions, and she could now represent rational numbers on a number line accurately. The real-life applications helped her see the relevance of rational numbers in her daily life, and she grew more interested in exploring other mathematical concepts.
Conclusion: The case study approach proved to be a successful way to engage Sarah and enhance her understanding of Rational Numbers. By connecting mathematical concepts to real-life scenarios, the teacher made the subject more relatable and meaningful for Sarah. As she progressed in her mathematics journey, Sarah’s solid grasp of rational numbers became the foundation for tackling more complex mathematical concepts in the future.
White paper on Class 8 Mathematics Rational Numbers
Abstract: This white paper aims to delve into the concept of Rational Numbers as taught in Class 8 Mathematics. Rational Numbers are a fundamental and practical aspect of mathematics that find applications in various real-life scenarios. The paper provides a comprehensive overview of the topic, including the definition, properties, operations, and applications of Rational Numbers. It also discusses the significance of this concept in shaping students’ mathematical skills and problem-solving abilities.
- Introduction: Class 8 marks a critical stage in a student’s mathematical journey, where they encounter the concept of Rational Numbers for the first time. Rational Numbers are numbers that can be represented as fractions, with both positive and negative values, as well as whole numbers and fractions. Understanding Rational Numbers lays the groundwork for more advanced topics in algebra, arithmetic, and various other fields of mathematics.
- Definition and Representation: In this section, we define Rational Numbers as the quotient or fraction of two integers and provide examples to illustrate their representation. We explore the concept of proper and improper fractions and discuss mixed numbers.
- Properties of Rational Numbers: We delve into the essential properties of Rational Numbers, such as closure, commutativity, associativity, and distributivity under addition and multiplication. We also discuss the additive and multiplicative identities and inverses of Rational Numbers.
- Operations with Rational Numbers: This section covers the fundamental operations performed with Rational Numbers, including addition, subtraction, multiplication, and division. We explain the rules for these operations and provide step-by-step examples to demonstrate the process.
- Simplification and Conversions: Here, we discuss simplification techniques for Rational Numbers, such as finding the lowest terms or converting improper fractions to mixed numbers and vice versa. Real-life applications of these conversions are highlighted.
- Representation on the Number Line: Visualizing Rational Numbers on a number line is a crucial skill for students. We explain how Rational Numbers are represented on the number line and demonstrate how to compare and order them.
- Real-Life Applications: This section showcases the practical applications of Rational Numbers in various fields, including finance, cooking, maps, time, and measurements. Examples of using Rational Numbers in everyday life scenarios are provided to emphasize their significance.
- Problem-Solving and Critical Thinking: The study of Rational Numbers fosters problem-solving abilities and critical thinking skills in students. We explore how rational numbers help students approach complex mathematical problems with confidence and precision.
- Conclusion: The exploration of Rational Numbers in Class 8 Mathematics lays a strong foundation for students to excel in higher-level mathematics. The practical applications of Rational Numbers in everyday life illustrate the relevance and importance of this concept. Understanding Rational Numbers equips students with essential mathematical skills and enables them to approach real-world challenges with a logical and analytical mindset.
- References: This section includes a list of references and resources used to compile the white paper, providing students, teachers, and educators with further reading materials on Rational Numbers.
This white paper serves as a comprehensive guide to Rational Numbers in Class 8 Mathematics, offering valuable insights and practical examples to enhance students’ understanding and appreciation of this fundamental mathematical concept.


